Category: Chicago

Categories
Chicago Economic History Suggested Reading Syllabus

Chicago. Reading list for Development of Monetary and Financial Institutions. Hamilton, 1960

 

 

The papers of the economic historian Earl J. Hamilton are a grab-bag of archival treasure, poorly sorted and demanding from the historian an unlimited faith in the goodness of the gods of serendipity. This post is a course reading list that would have rested safe in the obscurity of Hamilton’s papers, but for a chance encounter. I have taken the liberty of assuming the course title for Economics 334 at the University of Chicago in 1959-60 would match that of 1956-57. The course reading list is a nice example of the intersection of economic history and the history of economics.  

_____________________

Economics 334: Mr. Hamilton

Assignments to be read before May 20, 1960

  1. Luigi Einaudi, “The Medieval Practice of Managed Currency,” in A.D. Gayer (Ed.), The Lessons of Monetary Experience, pp. 259-268. HG 255.L63
  2. W. C. Mitchell, “The Role of Money in Economic Theory,” in The Backward Art of Spending Money, pp. 149-176. HB 33.M 68.
  3. Adam Smith, Wealth of Nations, “Digression concerning Banks of Deposit, particularly concerning that of Amsterdam,” in Book IV, Chapter III, Part I. HB 161. S 65.
  4. Earl J. Hamilton, American Treasure and the Price Revolution in Spain, Chapter XIII. H31.H33, v. 43
  5. Earl J. Hamilton, “Prices and Wages at Paris under John Law’s System,” Quarterly Journal of Economics, Vol. LI, (1936-1937), pp. 42-70. HB1.Q3
  6. Jacob Viner, Studies in the Theory of International Trade, Chapters III-V HF1007.V75
  7. N. J. Silberling, “Financial and Monetary Policy of Great Britain during the Napoleonic Wars,” Quarterly Journal of Economics, Vol. XXXVIII (1923-24), pp. 214-33, 397-439. HB1.Q3, v.38
  8. Lloyd W. Mints, History of Banking Theory, Chapter IV. HG1586.M6
  9. Walter Bagehot, Lombard Street. HG3000.L82B3
  10. R. S. Sayers, “The Question of the Standard in the Eighteen-Fifties,” Economic History (a supplement to the Economic Journal), Vol. II, pp. 575-601. HB1.E31
  11. Rufus S. Tucker, “The Myth of 1849,” in C.O Hardy, Is There Enough Gold? Appendix A, pp. 177-199. HG289.H28.
  12. J. H. Clapham, The Bank of England, Vol. II, Chapters VI-VIII and Epilogue. HG2996.C6
  13. Knut Wicksell, “The Influence of the Rate of Interest on Prices,” Economic Journal, Vol. XVII (1907), pp. 213-220. YW16 (reprint)
  14. O. M. W. Sprague, Crises under the National Banking System, Washington, 1910, pp. 1-107. HB3743.S7
  15. John Stuart Mill, Principles of Political Economy, Book III, Chapter XII. HB171.M635, M636, M644, M653.
  16. Charles F. Dunbar (Revised and edited by O. M. W. Sprague), The Theory and History of Banking, Chapters VIII (“The English Banking System”), IX (“The French Banking System”), X (“The German Banking System”), XI (“The National Banks of the United States”). HG1586.D9
  17. J. M. Keynes, A Tract on Monetary Reform, Chapters I-II, IV-V. HG221.K4
  18. J. M. Keynes, A Treatise on Money, Vol. II, Chapter 30. HG221.K422.

There will be an hour examination on April 29, 1960 covering 1-18 and the lectures.

  1. Alfred Marshall, Money, Credit, and Commerce, Books II, IV, and Appendix A. HG221.M35
  2. J. M. Keynes, Essays in Persuasion, Part II, Chaps. 1 and 3; Part III, Chapter 5; Part V, Chapter 2. In the London, 1933 edition these chapters cover pages 77-79, 105-17, 244-70, 358-73. HC57.K471.
  3. D. H. Robertson, Essays in Monetary Theory, Chaps. I and XII. HB 171.R544.
  4. Fred H. Klopstock, “Monetary Reform in Western Germany,” Journal of Political Economy, August, 1949. HB1.J7, v. 57.
  5. J. M. Keynes, A Treatise on Money, Vol. II, Chaps. 35 and 37. HG221.K422
  6. Earl J. Hamilton, “Prices and Progress,” Journal of Economic History, XII (1952), pp. 325-49.
  7. J. M. Keynes, The General Theory of Employment, Interest and Money, Chapter 23. HB171.K46
  8. Official Papers by Alfred Marshall, pp. 3-16. HG171.M318.
  9. The Federal Reserve System: Purposes and Functions
  10. Rondo E. Cameron, “The Credit Mobilier and the Economic Development of Europe,” Journal of Political Economy, LXI (1953), pp. 461-88.

There will be a three-hour final examination (9:00-12:00) on May 27, 1960 covering all assignments and lectures.

Source: Duke University. David M. Rubenstein Rare Book and Manuscript Library. Earl J. Hamilton Papers. Box 2. Folder “Academic and Personal Correspondence 1950s-1970s; 1990; and n.d.”

Image Source:  University of Chicago Photographic Archive, apf1-02446, Special Collections Research Center, University of Chicago Library.

Categories
Berkeley Chicago Faculty Regulations Harvard Johns Hopkins M.I.T. Michigan Rochester Stanford Uncategorized Yale

Harvard. Report on the General Examination for an Economics PhD, 1970

 

 

What makes this report on the general examination in the economics PhD program at Harvard particularly valuable is its brief survey of the practice at eight other universities: Yale, MIT, Johns Hopkins, Rochester, Stanford, Berkeley, Michigan, and Chicago. 

_____________________

DRAFT

This draft is distributed in Professor Chenery’s absence to permit discussion at the next Department meeting, January 27, 1970.
Professor Chenery or other members of The Committee might wish to record further comments in preparation [of] a final report.

*  *  *  *  *  *  *  *

HARVARD UNIVERSITY
DEPARTMENT OF ECONOMICS

Cambridge, Massachusetts 02135
January 16, 1970

To: The Department of Economics
From: Committee on Graduate Instruction

REPORT ON THE GENERAL EXAMINATION FOR THE PH.D.

In response to a number of requests from students and faculty, the Committee has reexamined at considerable length the requirements for the General Examination. This report summarizes our general assessment in section I and makes specific recommendations for changes in section II. Some related issues needing further consideration are listed in section III.

Although for the past several years graduate students have criticized various aspects of the generals, the main source of dissatisfaction seems to be with the rigidity of “the system” rather than with any particular aspect of it. We have taken advantage of the fact that the Committee now has three student members to try to understand some of the effects of our present procedures on students’ choices and incentives. We have also tried to strike a better balance between preparation for the general examination and other aspects of a student’s training in his first two years.

As a background for our discussion, the secretary of the Committee compiled a useful summary of the regulations in effect at other leading universities, which is attached.

 

ROLE OF THE GENERAL EXAMINATION

The primary functions [sic] of the General Examination is to evaluate the student’s formal preparation in economics before he proceeds to more advanced phases of teaching and thesis preparation. It also serves as a screening device to weed out weak candidates, as a basis for subsequent recommendations for employers, and as an indirect way of organizing the student’s course work in his first two years. These multiple functions produce much of the debate over requirements at Harvard and elsewhere, since a system that is ideal for one purpose has weaknesses for another.

One of the main criticisms of the existing Harvard system is its psychological impact on the student. The need to satisfy the requirements in all fields within a period of several months inhibits most students from exploring non-required topics until after they have passed the generals. On balance, we are impressed with the desirability of adopting a more flexible timing that will encourage the student to get most of his tool requirements out of the way in the first year and use the second year to explore the fields of his special interest and get some taste of actual research. We have tried to maintain the undoubted benefits of an overall examination, however, as compared to a set of course requirements.

Our survey of other departments shows a significant trend toward breaking down the requirements into separate parts and focusing less on the culminating oral examination. Most departments use the qualifying examination in theory as a device for screening first year students, which also reduces the burden of preparing all fields in the second year. In most departments the minimum proficiency in quantitative techniques and economic history is demonstrated by a satisfactory course grade rather than by inclusions in the general examination. Although we have made our own judgements on these questions, we recommend movement in these directions.

Another consideration which makes greater flexibility desirable is the growing proportion of students who are already well prepared in one or more required fields. For many students, the present system therefore encourages too much review of material they have already covered. We feel that those who are adequately prepared on one of the required fields (theory, quantitative method, history) should have an opportunity to satisfy this requirement in their first year in order to make better use of their time thereafter.

Our recommendations are directed toward achieving greater flexibility in the timing of courses and examinations to allow the student to make more effective use of his time. This should enable many students to get started earlier on their optional fields and to make a better choice of their field of specialization. We do not envision any reduction in the total work done in the first two years or any lowering of standards of performance.

 

SPECIFIC RECOMMENDATIONS

General Principles

  1. The general examination should be separated into four component parts—theory, quantitative method, economic history, and special fields—each of which would be graded separately.
  2. The minimum requirement in quantitative method and economic history should be regarded as a “tool requirement” or “literacy test” as has become the practice in the quantitative field. Students wishing to specialize in these fields may offer them at a higher level as one of their special fields.
  3. The term “general examination” would apply to the oral examination on the special fields. (The question of a general grade on all parts as at present was left open.)
  4. There should be no prescribed timing of the four components, other than the stipulation that the required fields be either completed (or write-off courses in progress) at the time of the oral examination on the special fields. Qualified students would be encouraged to complete one or more requirements in the first year.
  5. Two write-offs should be allowed rather than one.
  6. A subcommittee would be set up for economic history (and retained in theory and quantitative method). The standards and ways of satisfying them in the three required fields should be proposed by the three subcommittees and ratified by the GIC and the Department.

The Theory Requirement

  1. The present coverage (roughly 201a, 201b, 202a) should be retained. The examination would continue to be written.
  2. The examination should be offered two or three times a year. (A straw vote by students showed a preference for June, September and January and a margin for September over January.) Most students would take the examination at the end of their first year—in June or September.

The Quantitative Requirement

  1. The present de facto standard of the written examination should be accepted as the “literacy test”.
  2. The requirement can be met either by the present type of written examination (given twice a year) or by a grade of B+ in 221b or 224a. (It is estimated that roughly 75% would be able to qualify by course examination.)

The Economic History Requirement

  1. The history requirement be made parallel to the quantitative requirement in that:
    1. It can be satisfied by course or special departmental examination.
    2. It can either be offered at a minimum level or at a higher level as a special field.
  2. The minimum requirement would be satisfied by a course grade that would allow a similar proportion to qualify in this way (B+ or A- pending further information).
  3. Alternatives to the present 233 sequence (if any) to be established by the history subcommittee.
  4. Minimum standards in both history and quantitative method could be demonstrated by course examination.

The Requirement in Special Fields

  1. Two special fields would be required as the basis for the oral examination, which would also cover general analytical ability.
  2. Advanced theory, econometrics and economic history would be eligible as special fields, but the first two could not both be included. (In the majority view, one applied field apart from history would be required in order to eliminate the possibility of a candidate offering only the three required fields.)
  3. The candidate would be encouraged (or required?) to submit a research paper to be made part of the subject matter and record of the general examination (He is now “expected” to have presented a paper to a working seminar by the end of his second year.)
  4. The general oral examination would normally be taken at the end of the second year, but could not be taken before the qualifying exams in theory, quantitative and history have been passed (or prospective write-offs are in progress.)

QUESTIONS OF GRADING

  1. Should all examinations be either pass-fail or on a more limited grading scale than at present?
  2. Should the passing standard for the course option in both quantitative methods and history be B+?
  3. Should the four requirements be graded separately or combined (as at present) into an overall grade on the General Examination? (The committee favors first the alternative, but would also require “distinguished” performance in at least one area.)

*  *  *  *  *  *  *  *

Examination Requirements at Other Places

Below I summarize examination requirements at eight other places, including Yale, MIT, Hopkins, Rochester, Stanford, Berkeley, Michigan and Chicago. The main findings of the survey are:

  1. It appears that the massive type of “generals” (where all fields and theory are combined in one session) has almost disappeared. With the exception of Hopkins, all of the above schools seem to settle the theory examination at the end of the first year, with special fields examined at the end of the second year.
  2. Among the schools surveyed, only Yale has a written examination in history. Hopkins, Stanford, Chicago and Berkeley require a course, with “satisfactory” grade. MIT and Rochester have no requirement.
  3. Only Yale gives a written in quantitative aspect of the generals. All the other schools have course requirements (satisfactory grade) only.
  4. Practices vary with regard to number of special fields and type of examination. MIT and Hopkins require three, the others two special fields. Examinations at Yale are oral, at the other places written, in some cases both written and oral. In most places the special field examinations must be taken together, but in some (Rochester, Chicago) they can be separated. Throughout, these special examinations seem to be given by the department, and not merely as course examination.
  5. Some provisions of special interest:
    1. Chicago and Rochester’s second year research paper as part of general examination
    2. Stanford’s requirement for distinction in at least one field.

 

I. Yale

Comprehensive Examination

  1. Written examination in theory and econometrics, usually August or September after first year.
  2. Written examination on economic history; usually late spring of second year.
  3. Oral examination in two applied fields, chosen from six and in general analytical ability; late spring of second year. Given by four examiners. Student excused from general examination in special field courses at end of second year. Oral examination in theory, history, quantitative or field outside economics may be substituted for one of the applied fields if candidate has done year’s course work in applied field “with sufficient distinction”.

History and Quantitative

  1. History—written, end of second year, and option to substitute for one special field.
  2. Quantitative—written, end of first year, and option to substitute for one special field.

Other requirements

  1. Has apparently been dropped.
  2. One course credit of explicit research training, second year.
  3. Dissertation to be completed in fourth year.

 

II. MIT

General examination

  1. General examination in theory consists of two written papers—micro and macro, given in final exam period of first year. May be substituted for final examinations in theory courses.
  2. General examination normally at end of second year. Consists of:
    1. written examinations on three of 12 special fields. These may include advanced theory, econometrics or economic history.
    2. oral examination in the three fields after written.
    3. a fourth field is required but may be written off by B grade in full year course.

History and Quantitative

  1. History—no requirement. May be a special field.
  2. Quantitative—no generals examination. May be a special field.

Other requirements

  1. Two languages

 

III. Johns Hopkins

First Year Oral Examination

A first year oral examination is given in the spring of the first year, covering the fields in which the student has worked during that year.

Comprehensive Examination

Normally taken in spring of second year. Consists of:

  1. Two written examinations in theory, micro and macro.
  2. Three written examinations in special fields, one of which may be outside economics.
  3. Oral examination: Covers theory, special fields, statistics.

History and Quantitative

  1. History—satisfactory work in course.
  2. Statistics—satisfactory work in course.

Other Requirements

  1. One language.
  2. In addition to the departmental special examination, an examination is given by the graduate board, which includes members of other departments.

 

IV. Rochester

Qualifying Examination

  1. Theory and econometrics courses are required but are not part of Qualifying Examination.
  2. Qualifying Examination taken in May of second year. Consists of
    1. Written examination in two fields. These may include mathematical economics and econometrics. Need not be taken simultaneously.
    2. A second year research paper which is to be presented to a departmental seminar at the end of second year.
    3. After (a) and (b) are met, an oral examination in the special fields.

History and Quantitative

  1. Econometrics and mathematical economics requirements (courses), extent depending on fields.
  2. No history requirement.

Other Requirements

  1. Certain distribution requirement.
  2. Language and mathematics.

 

V. Stanford

Comprehensive Examination

  1. Written in micro and macro theory at end of first year. Cover course materials.
  2. Selection of special fields under two plans:
    1. If no minor subject is taken, student chooses four out of ten fields. These may include history, econometrics, mathematical economics. One field may be outside economics.
    2. Student may choose a minor subject (in another department) and choose only one out of the ten special economics fields.

Comprehensive written examinations for each field scheduled annually, usually at close of course sequence. Must show distinction in at least one field.

History and Quantitative

  1. History—Include at least two courses from offerings in economic history, history of thought, comparative economics, development.
  2. Quantitative—Econometrics course required.

Other Requirements

  1. Language or particular quantitative skills.
  2. Two seminars and research papers.

 

VI. Berkeley

Departmental Examination in Theory

  1. Must be passed by end of first year. Students with strong background take it in November of first term, others in June (end of first year).
  2. Written qualifying examinations given in two out of thirteen special fields at end of second year. Examinations given twice a year, must be taken together.
  3. Within one year after written qualifying examinations are completed, student presents himself for oral, based on prospectus (and interim results) of his thesis. General assessment of competence.

History and Quantitative

  1. Course in economic history at 210 level.
  2. Course in statistics at 240 level.

Other Requirements

  1. No language.

 

VII. Michigan

Preliminary Examination

  1. At end of theory courses in micro and macro, an “augmented examination” is given which serves as preliminary examination in theory.
  2. Two fields of specialization are required. One field is satisfied by satisfactory grades in two courses. For the other field a written preliminary examination is required.
  3. After this, oral examination on research topic and surrounding area.

Economic History and Quantitative

  1. No history requirement.
  2. Course requirement in statistics and econometrics.

Other Requirements

  1. No general language requirement.

 

VIII. Chicago

Preliminary Examination

  1. A “course [sic, “core” probably intended] examination” covering micro and macro theory is given twice a year (separate from course examinations) and is usually taken at end of first or middle of second year.
  2. Two special fields are chosen. Written examinations in these fields, separate from course examinations. Need not be taken together.
  3. Student presents a thesis prospectus before thesis seminar, usually in third year. Must pass on this for candidacy.

History and Quantitative

  1. History course required as part of distribution requirements.
  2. Course work in statistics required.

Other Requirements

  1. Math, no languages.

 

Source: John F. Kennedy Presidential Library. John Kenneth Galbraith Papers. Series 5. Harvard University File, 1949-1990. Box 526. Folder “Harvard University Department of Economics: General Correspondence, 1967-1974 (2 of 3)”.

Image Source: Harvard Class Album, 1946.

Categories
Chicago Economists

Columbia. PhD alumnus. William J. Shultz, 1924

 

Today we meet a Columbia Ph.D. alumnus who was brought to the Department of Political Economy at the University of Chicago in 1926 by Paul H. Douglas. He was mentioned in the course description of the previous post. Both Douglas as well as the University of Chicago publications people consistently misspelled William J. Shultz’s last name as “Schultz”. We can be sure that the correct spelling of the last name is without the Chicago “c”. Cf. both the Columbia College yearbook of 1922 and his obituary in the New York Times (below).

While Shultz did not write a dissertation in economics, he immediately produced a work on inheritance taxation that  won him the first prize in the Hart, Schaffner and Marx prize in economics. He went on to teach economics and later marketing.

While the New York Times obituary (see below) stated that Shultz was an assistant professor at the University of Chicago in 1926, the University of Chicago’s Annual Register covering the Academic Year Ending June 30, 1926, with Announcements for the Year 1926-1927 (p. 137) gives his rank as “instructor” for the summer quarter of 1926 and lists him as “lecturer” for the 1926-27 academic year.

Shultz is a nice specimen of the utterly brilliant young graduate whose great expectations resulted in just a pretty good career without leaving a lasting impression in the history of economics.

____________________________

Abstract of Shultz’s dissertation

“The book written by William J. Shultz introduces us to the Humane Movement in America that is dedicated to the protection of animals and children. It represents a continuation of an older work by Professor Roswell C. McCrea. At the present time in America there are 539 organizations with approximately 200,000 members active in this movement: 307 link the protection of animals with the protection of children and 175 are dedicated strictly to the protection of animals. The common motive here is the Prevention of Cruelty. The author documents the development of these organizations during the period 1910-1922, together with the organizational structures, methods of fund-raising and their inner-workings….”

Source: Own translation of the review by Agnes v. Zahn-Harnack published in Zeitschrift Für Die Gesamte Staatswissenschaft, 80(2), 379-380.

____________________________

Links to copies of books by William J. Shultz available on-line.

The Taxation of Inheritance. Boston: Houghton Mifflin Company, 1926.

American Public Finance (3rd edition). New York: Prentice-Hall, 1946.

Outline of Marketing. Ames, Iowa: Littlefield, Adams & Co., 1956.

American Marketing. San Francisco: Wadsworth Publishing Company, 1961.

____________________________

Paul Douglas on William J. Shultz (1925)

The University of Chicago
The School of Commerce and Administration

October 22, 1925

Professor J.A. Field
Faculty Exchange

My dear Field:

I quite forgot the other day in the Department meeting to suggest Dr. William J. Schultz [sic] as a person that I thought we ought to keep our eye on.

I got acquainted with Schultz’s work last year as a result of his application for an Amherst Memorial Fellowship and he seemed to me the most brilliant youngster that I have ever known, with the exception of Viner. Schultz took his Ph.D. at Columbia in 1924 at the age of 23. He wrote his dissertation on “The Humane Movement in the United States” which was published in the Columbia Studies. In addition to that, he has translated the important portions of Rignano’s book on the inheritance tax and Knopf has published this with an introduction by Seligman. On top of all this, in collaboration with another person he has written a history of commerce; while he submitted last June a manuscript on the inheritance tax in the Hart, Schaffner & Marx series, which Viner tells me was easily the best in its completed form. Viner thinks it was really a marvelous piece of work.

In addition to all this, Schultz is an accomplished musician and has command over some four or five European languages. He spent a summer in Mexico and has written on that country.

During the last year he was teaching at Hunter College but had some thought this year of going to Japan if he received an appointment at one of the universities there.

I met him and liked him very much. Seligman thinks him very brilliant, although one or two men at Columbia complained of his artistic temperament. I was in favor of his receiving an Amherst Fellowship, but the business men on the committee were afraid of his precocious brilliance and were fearful that he might “blow up.” It may be that he is somewhat unsteady, although I detected no signs of it. On the other hand, he is certainly close to being a genius, and there are all too few of those in economics. It would be a great card for us to get him in the Department, or in some way attached to the University of Chicago. It would be easier to get him before he wins the Hart, Schaffner & Marx prize, if he does.

He seems to be a person that we should fish for and that at the very least we should try to get him for next summer and then possibly we might also make connections with him for a later engagement.

Faithfully yours,

[signed] Paul H. Douglas

Source: The University of Chicago Archives. Department of Economics. Records. Box 6, Folder 7.

____________________________

1922 Columbia College Yearbook
William J. Shultz….BROOKLYN, N.Y.

Freshman Fencing Team (1), Morningside (3), History Club (2)(3)(4), Junta (3), Assistant in History Department (4).

Bill enjoys the distinction of being the only Columbia man who raised a mustache at the age of eighteen. He is also quite proud of his curly locks. “That,” said Bill as he pointed to one of his raven curls, “is what makes ‘em fall.” Bill is also a history shark. He can tell you when Abe Lincoln first donned long trousers and what size collar Napoleon wore at Waterloo. If Bill can do other things as well as he can sell books, he will not only read history but also make it.

Source: The 1922 Columbian, p. 153.

____________________________

Obituary

WILLIAM J. SHULTZ OF BARUCH SCHOOL
The New York Times, May 29, 1970

Dr. William J. Shultz, economist and author, who retired in 1964 as professor of business administration at the Bernard M. Baruch School of Business Administration of the City University of New York, died Saturday of a heart attack in Camden, Me. He was 68 years old and lived in New Harbor, Me.

Dr. Shultz was the author of several books in his field, the last of which was “American Marketing,” published in 1961.

He was born in Brooklyn on April 25, 1902, and graduated in 1922 from Columbia College, where he was a member of Phi Beta Kappa. He received a Ph.D. degree from Columbia University in 1924 and an LL.B. degree from New York Law School in 1930.

Early in his career he lectured on history at Columbia and taught history at City College and social science at Hunter College. He was assistant professor of economics at the University of Chicago in 1926.

Dr. Shultz was a financial consultant to the National Industrial Conference Board from 1926 to 1930, and joined the faculty of Baruch School in 1932.

His widow, Luisa, survives.

Image Source: The 1922 Columbian, p. 153.

Categories
Chicago Courses

Chicago. Empirical seminar on wages announcement. Douglas, 1926

Douglas

 

I had to consult the course announcements for 1926-27 to be sure that the course description I found in the files corresponded to that announced in the following letter from Paul H. Douglas to his chairman L. C. Marshall. We can be reasonably sure that the fifth person participating in the course was the recent Columbia Ph.D., William J. Shultz. I come to this conclusion because there is a letter in the same folder in which Douglas strongly recommends hiring William J. Schultz [sic].  The correct spelling turns out to be S-H-U-L-T-Z, and there is a New York Times obituary for William J. Shultz who was reported there to have taught economics at the University of Chicago in 1926.

____________________

The University of Chicago
The School of Commerce and Administration

July 23, 1926

My dear Mr. Marshall:

I enclose a brief and somewhat uninspired statement of a course on Wage Theory which I think may nevertheless serve as sufficient announcement to the students. Will you fill in the appropriate number of the course and the hours at which it is to be given? I would prefer two two hour sessions to four one hour.

            I will meet with Millis, Stone, and Viner in the fall to get their cooperation in the matter.

With all best wishes,
Faithfully yours,
[signature by w] Paul H. Douglas
Paul H. Douglas

PHD-W

____________________

Econ. 443

SPECIAL STUDIES IN WAGES
[1926-27, Winter quarter]

An attempt to frame a theory of wages and of distribution and to ascertain inductively some of the forces which determine the rate of wages. After a review of various wage theories, such as those of the marginal productivity, wages fund, discounted marginal productivity, subsistence, bargain, employment and vulgar theories, an analysis of the problem will be made in terms of the relative elasticity of the supply cures of the factors of production and of their curves of imputed productivity. An attempt will then be made to trace inductively in so far as possible the supply curves of labor and capital. The effect of wages upon the short-run supply of labor will be tested as regards a number of factors including: (1) the age of entrance into industry, (2) the age of departure from industry, (3) the proportion of persons within the active age groups gainfully employed, (4) hours of work, (5) absenteeism and turnover, (6) intensity of effort, (7) changes in skill, (8) immigration. The effect of changes in real wages upon the long-time supply of labor will also be tested as regards its influence upon (1) the birth rate in Great Britain and the United States, (2) the rate of net fertility, (3) the effective labor supply, (4) the percentage of unemployment.

If time permits, investigations will also be carried through on the probable nature of the supply curve of capital. After a review of the doctrine concerning saving that have been advanced by such writers as Ricardo, Senior, Mill, Cairnes, Sargent, Rae, Böhm-Bawerk, Laundry, Fisher, Cassell, etc., inductive tests will be made of the relationship between changes in the interest rate and changes in the amount of capital saved. The movement of the interest rate in Great Britain and the United States will first be studied. Indexes of capital growth in Great Britain and the United States in physical terms will then be constructed and the rates of change in the volume of saving will be compared with the rates of change in the interest rate. The probable supply curves of natural resources and of management will also be considered but because of reason of time cannot be investigated in detail. It is hoped that the work will make the probably nature of the supply curves of the factors clearer and thus help to establish a more inductive basis for the theory of distribution.

Each student will be expected to do some piece of research upon a problem connected with the general investigation.

Prerequisites–Economics 211, 240 and 301. Professor Douglas, in charge, with Messrs. Millis, Viner, Stone, and [William J.] Schultz [sic, correct spelling is Shultz] cooperating.

Source: The University of Chicago Archives. Department of Economics. Records. Box 6, Folder 7.

Image Source: University of Chicago Photographic Archive, apf1-05851, Special Collections Research Center, University of Chicago Library.

Categories
Chicago Economist Market Economists Teaching

Chicago. Laughlin’s observations on state of economics department, 1924

 

This post features a memorandum from 1924 that summarizes a conversation between the president of the University of Chicago and the first head of the department of political economy called in after retirement to help the department in covering a vacancy in its professorial ranks. Among other things we learn that Laughlin’s pension from the university was $3000/year.

Backstory 1: Shortly after being promoted to professor of economics, Harold G. Moulton left the University of Chicago in September 1922 to head the Institute of Economics established by the Carnegie Corporation in Washington, D.C. The department had trouble finding a successor, so among temporary measures it brought James Laurence Laughlin out of retirement during the academic year 1924-25 to help cover the money field. The last item transcribed below summarizes Laughlin’s observations on the state of the department ca. eight years after his retirement in 1916.

Backstory 2: L. C. Marshall’s request to resign both the Deanship of the school of Commerce and Administration [succeeded by W. H. Spencer] and school of Social Service Administration [succeeded by Edith Abbott] was accepted to take effect 31 December 1923. He agreed to continue on as Chairman of the Department of Political Economy under the condition that funds be provided for additional clerical services.

____________________

Letter from Chairman L. C. Marshall to President Ernest D. Burton

The University of Chicago
Department of Political Economy

June 1, 1924

My dear Mr. Burton:

The department of Political Economy sees no way of filling Mr. Moulton’s place in terms of the present situation. We turn, therefore, to temporary measures.

As one phase of the matter, will you approve of bringing Mr. Laughlin back for the Autumn Quarter, in case he is available? The 1924-25 budget contains the funds. I am at this same time asking Mr. Plimpton what would be involved as far as the relationship of stipend to retiring allowance is concerned.

A carbon of this letter is going to Mr. Tufts and Mr. Laing for their information.

Yours very sincerely,
[signed] L C Marshall

LCM:OU

____________________

Letter from Chairman L. C. Marshall to Nathan C. Plimpton, comptroller

The University of Chicago
Department of Political Economy

June 2, 1924

My dear Mr. Plimpton:

In case Mr. J. L. Laughlin should be engaged to give work with us this coming Autumn Quarter would his compensation for this work be in addition to his retiring allowance for that period, or would the allowance be discontinued for that period?

The department is thinking in terms of a stipend of about $2500 if his allowance continues. If it does not, probably $3000 would suffice even though this would less than $2500 plus allowance.

Yours very sincerely,
[signed] L C Marshall

LCM:OU

____________________

Letter from Chairman L. C. Marshall to President Ernest D. Burton

The University of Chicago
Department of Political Economy

May 29, 1924

President Ernest DeWitt Burton
The University of Chicago

My dear Mr. Burton:

This is a request to include in the Political Economy budget for the year 1924-25 the sum of $1,500.00 for clerical assistance.

In order that you may not need to consult files I give below an abstract of the situation up to the present time.

  1. Along about January 1 you expressed a willingness to take up with the expenditures committee the provision of clerical assistance. While you were on your vacation I took the matter up through Mr. Dickerson and a sum was granted providing for clerical assistance during the remainder of this current budgetary year.
  2. I asked Mr. Tufts to insert in the 1924-25 budget a request for $1,500.00 but he indicated the need of awaiting your return before taking action on the matter.
  3. Sometime after your return I asked Mr. Tufts whether he wished to take the matter up with you or whether I should take it up. The reply received indicated that Mr. Plimpton was under the impression that you had some understanding on the matter.
  4. The official copy of the budget received from Mr. Tufts a day or two ago contains no such item.

Yours very sincerely,
[signed] L C Marshall

LCM:EL

____________________

Carbon copy of letter
from President Ernest D. Burton to L. C. Marshall

June 4, 1924

My dear Mr. Marshall:

In reference to your letter of May 29 I am glad to be able to state that the budget of next year as approved by the Board of Trustees carried with it an appropriation of $1500 for clerical service for your department. The statement sent to you by Mr. Tufts was intended to cover only the salaries of the teaching staff.

I am sure the Board of Trustees would approve the recommendation of the department that Mr. Laughlin be invited to give lectures in the autumn quarter. As respects his compensation, concerning which you wrote to Mr. Plimpton, the custom has been to add a stipend for such service to the retiring allowance which is continued without interruption. Mr. Small [Department of Sociology] and Mr. Coulter [Department of Botony] are both being retained next year on this basis, each of them rendering substantially half service throughout the year. The extra compensation is, in one case, $1500, in the other $2000. May I raise the question whether either sum would not be sufficient in Mr. Laughlin’s case also? In other words, $2000 for the special service, in addition to the $3000 of his regular retiring allowance?

Very truly yours,

Mr. L.C. Marshall
The University of Chicago

EDB:HP

____________________

Memorandum of Conversation with
Professor Laughlin
—November 19, 1924

On returning to the University Mr. Laughlin is struck with two things in respect to the Department of Political Economy.

1) The introductory courses are not as well conducted as they were in 1916. Then some of the abler men of the department were giving them. Now they are largely in the hands of instructors and assistants.

2) There has been a large increase in the number of graduate students.

There are four Universities that have graduate departments in Political Economy that need to be taken into account by us.

Columbia has the largest department.

Chicago is second in size.

Harvard is falling off.

Wisconsin is falling off.

            The task of meeting graduate students and overseeing their work is an arduous one. We must, however, hold our own in dealing with this class of students. It would be desirable to raise the level of undergraduate work, but not at the expense of sacrificing our graduate work.

We must hold our present staff. Marshall, Clark and Viner are the best men. Wright is a good man. Field and Millis are pretty set in their ways, but this whole staff should be retained.

(In subsequent conversation with Marshall he said Field was the best man of the whole group, but that his Harvard inhibitions made it impossible for him to bring things to pass. He is afraid of what people will say and of the tendency of things. Millis is a good man, but no longer capable of much re-adjustment.)

Mr. Laughlin urges that we must get a first class man in money. He believes that the business interests should be asked to give money for this particular purpose.

The weakness of the undergraduate department is due to the lack of good men and salaries to pay them. C & A is doing most of the undergraduate work. This is not in itself objectionable. The spirit of C & A is good.

It is very desirable to unify the Department of Economics and the School of Commerce and Administration further.

 

Source: The University of Chicago Archives. Office of the President. Harper, Judson and Burton Administration Records. Box 23, Folder 6 “Department of Political Economy, 1894-1925) Part 2”

Image Source: University of Chicago Photographic Archive, apf1-03687, Special Collections Research Center, University of Chicago Library.

Categories
Chicago Funny Business

Chicago. A Mikado parody number. Probably 1949.

 

Among the papers of Alfred Rees at the Economists’ Papers Archive at Duke and of Milton Friedman at the Hoover Institution Archives, one finds stapled copies of a skit written by graduate students at the University of Chicago with the title “Alice in Stationary State”. The cover page includes a list of 18 contributors to the skit either as librettist and/or as a performing member of the cast/chorus. Carl Christ who was to leave Chicago and join the faculty of the Department of Political Economy at Johns Hopkins University in 1950 was named as a member of the cast/chorus. The mimeographed manuscript bears no date, but in Christ’s paper “The Cowles Commission’s Contributions to Econometrics at the University of Chicago, 1939-1955 (Journal of Economic Literature, Vol. XXXII, March 1994, pp. 30-59) two songs from the manuscript are quoted by Christ, one to the tune of “The American Patrol“. Since he dates the skit to about 1949 and we know his whereabouts for 1950, I think it is safe to trust his memory as to the 1949 date he mentions. Note the slight discrepancies with presumably a later, recycled version of the lyrics.

Other parodies of Gilbert and Sullivan that have been transcribed for Economics in the Rear-View Mirror include:  “When I was a Lad“, “The Major General’s Song” and “I’m Called Little Buttercup” . Non-Gilbert-Sullivan material  transcribed from the skit are the Song for an Entrepreneur (to the tune of “Jingle Bells”) and “First Epistle unto the entering students” .

Here is a link to a YouTube clip from the Mikado for those of us whose familiarity with Gilbert and Sullivan lyrics is not quite up to mid-20th century Chicago levels.

_____________________

DECONTROL SONG
(to the tune of “My Object all Sublime from Patience (sic*))

*Actually from Gilbert and Sullivan’s Mikado.

A more humane economist never
Did in Chicago exist;
To nobody second,
He’s certainly reckoned,
A true philanthropist.
‘Tis his most human endeavor
To make to some extent
Each individual
Tenant pay the
Equilibrium rent.		 A more humane Mikado never
Did in Japan exist,
To nobody second,
I’m certainly reckoned
A true philanthropist.
It is my very humane endeavor
To make, to some extent,
Each evil liver
A running river
Of harmless merriment.
CHORUS:

His object all sublime
He might achieve in time,
Convict the planners of their crime,
The planners of their crime.
Make those of Leftist bent
Unwillingly represent
A source of innocent merriment, of innocent merriment.

 CHORUS:

My object all sublime
I shall achieve in time —
To let the punishment fit the crime —
The punishment fit the crime;
And make each prisoner pent
Unwillingly represent
A source of innocent merriment!
Of innocent merriment!
The addle-pated
Who aggregate the unrelated data
And find instead of
The alpha they seek
A beta even greater.
The Keynesians and all their ilk
Who seek to find
Nirvana…He’ll fix them all,
He’ll fix them all,
He’ll ship them to Urbana!		 All prosy dull society sinners,
Who chatter and bleat and bore,
Are sent to hear sermons
From mystical Germans
Who preach from ten till four.
The amateur tenor, whose vocal villainies
All desire to shirk,
Shall, during off-hours,
Exhibit his powers
To Madame Tussaud’s waxwork.
CHORUS:

His object all sublime
He might achieve in time,
Convict the planners of their crime,
The planners of their crime.
Make those of Leftist bent
Unwillingly represent
A source of innocent merriment, of innocent merriment.

 CHORUS:

My object all sublime
I shall achieve in time —
To let the punishment fit the crime —
The punishment fit the crime;
And make each prisoner pent
Unwillingly represent
A source of innocent merriment!
Of innocent merriment!

Source: Duke University. David M. Rubenstein Rare Book & Manuscript Library, Economists’ Papers Archive. Albert Rees Papers, Box 1, Folder “Personal”. Identical copy also found at The Hoover Institution Archives, Milton Friedman Papers, Box 79, Folder 6 “University of Chicago Miscellaneous.”

_____________________

Second, revised version

MEMBER OF THE FACULTY:
(to the tune of “My object all sublime” from the MIKADO)

A more humane economist never
In Chicago did exist;
To nobody second,
I’m certainly reckoned,
A true philanthropist.
It is my most human endeavor
To make to some extent
Each individual
Tenant pay the
Equilibrium rent.		 A more humane Mikado never
Did in Japan exist,
To nobody second,
I’m certainly reckoned
A true philanthropist.
It is my very humane endeavor
To make, to some extent,
Each evil liver
A running river
Of harmless merriment.
My object all sublime
I might achieve in time,
Convince the planners of their crime,
The planners of their crime.
Make those of Leftist bent
Unwillingly represent
A source of innocent merriment
Of innocent merriment.		 My object all sublime
I shall achieve in time —
To let the punishment fit the crime —
The punishment fit the crime;
And make each prisoner pent
Unwillingly represent
A source of innocent merriment!
Of innocent merriment!
The addle-pated
Who aggregated unrelated data
And found instead of
The alpha they sought
A beta even greata.
The Keynesians and all their ilk
Who seek to find
Nirvana…I’ll fix them all,
I’ll fix them all,
I’ll ship them to Urbana!		 All prosy dull society sinners,
Who chatter and bleat and bore,
Are sent to hear sermons
From mystical Germans
Who preach from ten till four.
The amateur tenor, whose vocal villainies
All desire to shirk,
Shall, during off-hours,
Exhibit his powers
To Madame Tussaud’s waxwork.

Source: The Hoover Institution Archives. Milton Friedman Papers, Box 79, Folder 6 “University of Chicago Miscellaneous.”

Categories
Chicago Exam Questions Suggested Reading Syllabus

Chicago. Theory of Distribution. Readings and exam questions. Metzler, 1961-64

 

In the early 1960s Lloyd A. Metzler taught a course at the University of Chicago that offered a mélange of production, capital, fiscal, growth and international trade theories as a/the “theory of distribution”. It is fascinating to see these very different theoretical streams converging on the topic of distribution. 

_________________________

ECONOMICS 302
Reading List—Spring, 1961

THEORY OF DISTRIBUTION
L. A. Metzler

Principal Topics and Suggested Reading

I. Production Functions and Income Distribution

Paul H. Douglas, “Are There Laws of Production?” American Economic Review, XXXVIII, No. 1, March 1948.

D. Gale Johnson, “The Functional Distribution of Income in the United States, 1850-1952,” The Review of Economics and Statistics, XXXVI, No. 2, May 1954.

Solomon Fabricant, Basic Facts on Productivity Change, Occasional Paper No. 63, National Bureau of Economic Research.

II. Capital and the Concept of Income

Knut Wicksell, Lectures on Political Economy, Vol. I, Part II.

Frank H. Knight, “The Quantity of Capital and the Rate of Interest,” Part 1, Journal of Political Economy, August, 1936, Part 2, Journal of Political Economy, October, 1936.

T. W. Schultz, “Investment in Human Beings Capital,” American Economic Review, March 1961.

Irving Fisher, The Theory of Interest (1906), reprinted by Kelley and Millman, New York, 1954.

III. Investment and Economic Growth

Evsey Domar, Essays in the Theory of Economic Growth, New York, Oxford University Press, 1957, Chapter 1.

Walter W. Rostow, The Process of Economic Growth, New York, 1952.

Trygve Haavelmo, A Study in the Theory of Investment, University of Chicago Press.

J. M. Keynes, The General Theory of Employment, Interest and Money, Chapters 11-14.

A. P. Lerner, “On the Marginal Product of Capital and the Marginal Efficiency of Investment,” Journal of Political Economy, February, 1953.

James Tobin, “A Dynamic Aggregative Model,” Journal of Political Economy, April, 1955.

IV. The Economic Consequences of Public Debt

James Buchanan, Public Principles of Public Debt, Irwin, 1958.

Lloyd A. Metzler, “Wealth, Saving and the Rate of Interest,” Journal of Political Economy, April, 1951.

Robert A. Mundell, “The Public Debt, Corporate Income Taxes, and the Rate of Interest,” Journal of Political Economy, December, 1960.

J. R. Hicks, “Mr. Keynes and the ‘Classics’: A Suggested Interpretation,” Econometrica, Vol. V, April 1937.

IV. International Trade and the Distribution of Income

Bertil Ohlin, Interregional and International Trade, Harvard University.

Wolfgang Stolper and Paul Samuelson, “Protection and Real Wages,” Review of Economic Studies, IX (1941), 58-73.

David Ricardo, Principles of Political Economy and Taxation, Chapter 7.

_________________________

ECONOMICS 302
Reading List—Spring, 1963
[same for Spring, 1964]

THEORY OF DISTRIBUTION
L. A. Metzler

I. Production Functions and Income Distribution

Paul H. Douglas, “Are There Laws of Production?” American Economic Review, XXXVIII, No. 1 (March, 1948).

D. Gale Johnson, “The Functional Distribution of Income in the United States, 1850-1952,” The Review of Economics and Statistics, XXXVI, No. 2 (May, 1954).

Solomon Fabricant, Basic Facts on Productivity Change, Occasional Paper No. 63, National Bureau of Economic Research.

Marvin Frankel, “The Production Function: Allocation and Growth,” American Economic Review, LII, No. 5 (December, 1962).

Kenneth Arrow, Hollis B. Chenery, Nigicha Minhas, and Robert M. Solow, “Capital-Labor Substitution and Economic Efficiency,” Review of Economics and Statistics, XLII, No 3 (August, 1961).

R. M. Solow, “A Skeptical Note on the Constancy of Relative Shares,” American Economic Review, XLVIII (1958).

II. Income, Interest, and the Concept of Capital

Knut Wicksell, Lectures on Political Economy, Vol. I, Part II.

Frank H. Knight, “The Quantity of Capital and the Rate of Interest,” Part I, Journal of Political Economy (August, 1936), Part II, Journal of Political Economy (Oct., 1936).

T. W. Schultz, “Investment in Human Capital,” American Economic Review (March, 1961).

Irving Fisher, The Theory of Interest (1906), reprinted by Kelley and Millman, New York, 1954.

David Meiselman, The Term Structure of Interest Rates, Prentice-Hall, Inc., 1962.

[Handwritten addition:] J. A. G. Grant, “Meiselman on the Structure of Interest Rates: A British Test,” Economica, New Series, Vol. XXXI, No. 121, Feb. 1964.

Friedrich A. Lutz, “The Structure of Interest Rates,” Quarterly Journal of Economics, 1940-41. Reprinted in American Economic Association, Readings in the Theory of Income Distribution (eds.) William Fellner and Bernard Haley.

J. R. Hicks, Value and Capital, Oxford at the Clarendon Press (2d ed.), Parts III and IV.

Lloyd A. Metzler, “Wealth, Saving and the Rate of Interest,” Journal of Political Economy, LIX, No. 2 (April, 1951).

Robert A. Mundell, “The Public Debt, Corporate Income Taxes, and the Rate of Interest,” Journal of Political Economy, LXVIII (December, 1960).

III. Production Functions, Innovations and Economic Growth

Evsey Domar, Essays in the Theory of Economic Growth, New York: Oxford University Press, 1957, Chapter 1.

Walter W. Rostow, The Process of Economic Growth, New York, 1952.

Trygve Haavelmo, A Study in the Theory of Investment, University of Chicago Press.

Hirofumi Uzawa, “On a Two-Sector Model of Economic Growth,” Review of Economic Studies, XXIX, No. 1 (1962).

T. W. Swan, “Economic Growth and Capital Accumulation,” Economic Record, XXXII (1956).

James Tobin, “A Dynamic Aggregative Model,” Journal of Political Economy (April, 1955).

IV. International Trade and the Distribution of Income

Wolfgang Stolper and Paul Samuelson, “Protection and Real Wages,” Review of Economic Studies, IX (1941).

Paul Samuelson, “International Trade and the Equalization of Factor Prices,” Economic Journal, LVIII (1948).

Paul Samuelson, “International Factor Price Equalization Once Again,” Economic Journal, LIX (1949).

Source: Duke University. David M. Rubenstein Rare Book and Manuscript Library. Economists’ Papers Archive. Papers of Lloyd A. Metzler, Box 9, Folder “Reading Lists 300A+B—302”.

_________________________

Economics 302
FINAL EXAMINATION
Spring Quarter, 1963

Lloyd A. Metzler
June 4, 1963

Answer all questions:

  1. Give the formula for the Cobb-Douglas production function and prove its implications with respect to the following:
    1. The effects of a uniform increase in capital and labor upon relative and absolute wages and interest rates on the assumption that competitive conditions exist in both the factor markets and the commodities markets.
    2. The effect of a rise in the ratio of capital to labor upon relative and absolute wages, and interest rates again on the assumption of competitive conditions.
  2. Answer the same questions for the C.E.S. production function.
    1. State what is meant by a production function which is homogeneous of the first degree.
    2. Show that if a production function possesses this type of homogeneity, the output per worker depends entirely upon the ratio of capital to labor, and not at all upon the scale of production.
    3. Prove that the Cobb-Douglas production function and the C.E.S. function are both homogeneous of the first degree.
  4. The U. S. Treasury wants to reduce the long-term interest rate so as to encourage investment and at the same time increase the short-term rate so as to prevent short-term capital outflows. For this purpose it has been shortening the term structures of the federal debt. That is, the treasury has been purchasing its long-term bonds and issuing short-term bonds as a substitute.
    1. Show how such an operation might be expected to achieve the desired results.
    2. In view of the expectations hypothesis investigated by David Meiselman, would you expect such an operation to achieve its purpose? Explain carefully.
    1. Distinguish between the expectations hypothesis concerning the term structure of interest rates and the liquidity preference hypothesis and show what each implies with respect to the term structure of interest rates.
    2. Which hypothesis does the historical evidence seem to support?
    3. Is there any way of reconciling the two views?
    1. Given the yield on long-term bonds, R1, R2,…, Rn, show how a series of expected forward rates for one-year bonds r1, r2, r3,…, beginning in years 1, 2, 3, can be derived from the yield table on long term bonds. What operations would a bond holder need to undertake in order to be sure that he would receive these expected forward rates in spite of changes in bond prices?
    2. Derive the formula for the yield of a three-year forward bond, with interest rates applicable at the end of the third year, and show again, how a bondholder can realize this yield through operations in the bond market, regardless of fluctuations in bond prices.

Source: Duke University. David M. Rubenstein Rare Book and Manuscript Library. Economists’ Papers Archive. Papers of Lloyd A. Metzler, Box 9, Folder “Exams 302”.

_________________________

ECONOMICS 302
COURSE EXAMINATION — SPRING, 1964

Lloyd A. Metzler
June 9, 1964
1:30—3:30

ANSWER ALL QUESTIONS

  1. In the theory of distribution, it is usual to assume that the production function for output as a whole is homogeneous of the first degree.
    1. What is the meaning of a homogeneous production function?
    2. Show that homogeneity implies that commodities are produced at constant cost.
    3. Show that if the production function is homogeneous of the first degree and all factors of production are paid according to the value of their marginal products, the total amount paid will be exactly equal to the total return.
    4. Is it necessary to have homogeneous production functions to prove this proposition? Why, or why not?
    1. Define “elasticity of substitution” and show what bearing it has on the distribution of income.
    2. The following is a table indicating indexes of units of capital k and the price of capital, pk, as well as the units of workers, w, and the price of workers, pw.
P Price of workers
(pw)		 Units of workers
(w)		 Price of capital
(pk)		 Units of capital
(k)
Period I 1.00 200 2.00 100
Period II 2.00 250 1.00 500

Does this table give any indication as to the elasticity of substitution? Why, or why not?

    1. Define the Cobb-Douglas production function and the C.E.S. production function and show that: Cobb-Douglas production function is homogeneous of the first degree with an elasticity of substitution equal to unity.
    2. Show that the C.E.S. production function is homogeneous of the first degree.
    3. Show that, when 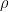\rho approaches zero the C.E.S. production function has an elasticity of substitution equal to unity.
    1. Define and evaluate the capital theories of the following economists:
      (1) T. W. Schultz
      (2) Irving Fisher
      (3) Knut Wicksell
      (4) F. H. Knight
    2. What are Knight’s objections to the notion of a period of production? Why does he believe there are no diminishing returns to the accumulation of capital?
    1. Derive the Harrod-Domar concept of a balanced state of growth, and show why it is inherently unstable.
    2. How is the concept of balanced growth related to Keynes’ theory of employment?
    1. Discuss the following theories of interest, and show how they are related to the term structure of interest rates.
      (1) Liquidity preference.
      (2) Expectations.
      (3) Constitutional weakness in the futures market.
    2. Does a downward-sloping term-to-maturity structure of interest rates conflict with the liquidity-preference theory? Why, or why not?
    3. Assuming that the interest rates for bonds of various maturities are as follows:
      year bonds R1
      2. year bonds R2
      3. year bonds R3
      4. year bonds R4
      5. year bonds R5
      6. year bonds R6
      7. year bonds R7
      8. year bonds R8
      Show how the implicit forward rates for short-term one year bonds r1, r2, r3, r4, r5, r6, r7, r8can be computed from the actual market yields, R1, R2, R3, R4, R5, R6, R7, R8.
    4. Assuming that the market rates are R1, R2, R3, R4, R5, R6, R7, R8, you are asked to derive the rate for a 3 year bond beginning in year 6 and show what market transactions the typical bondholder would have to make to insure that he actually received the interest rate implicit in this formula.

 

Source: Duke University. David M. Rubenstein Rare Book and Manuscript Library. Economists’ Papers Archive. Papers of Lloyd A. Metzler, Box 9, Folder “Exams 302”.

Source Image: Posting by Margie Metzler on the Metzler Family Tree at the genealogical website, ancestry.com.

Categories
Chicago Exam Questions

Chicago. Money, Prelim Exam for Banking and Monetary Policy, 1959

 

Preliminary examinations at the University of Chicago for Money, Banking and Monetary Policy from the Summer Quarter, 1956 and Winter Quarter, 1969 have been posted earlier.

On August 4, 1959 a three-hour “Core Examination” was taken by seventeen students and a four-hour “Money Prelim” was taken by nine students. Two additional questions were added to the “Money Prelim”.

_______________

Summer Quarter 1959 Examination Committee for Money, Banking and Monetary Policy:

Milton Friedman (chairman)
Earl J. Hamilton
Reuben A. Kessel

_______________

Reuben A. Kessel, obituary
New York Times, 21 June 1975.

Dr. Reuben A. Kessel, professor of economics at the University of Chicago’s Graduate School of Business since 1962, died yesterday at a hospital in Chicago, after having suffered a stroke a week ago. He was 52 years old and lived in Floss moor, Ill.

Dr. Kessel earlier taught at the University of Missouri and the University of California at Los Angeles. From 1952 to 1956 he was an economist with the Rand Corporation. He later served as research associate with the National Bureau of Economic Research here. He joined the Chicago faculty in 1957.

He was the author of “Cyclical Behavior of the Term Structure of Interest Rates.”

He received an M.B.A. degree in 1948 and a doctorate in 1954, both from Chicago.

Surviving are his widow, a daughter and two brothers.

_______________

CORE EXAMINATION
MONEY, BANKING AND MONETARY POLICY

Preliminary Examination for the Ph.D. and A.M. Degrees
Summer Quarter 1959
[August 4]

WRITE THE FOLLOWING INFORMATION ON YOUR EXAMINATION PAPER

Your Code Number and NOT your name
Name of Examination
Date of Examination

Results of the examination will be sent to you by letter.

Answer all questions. Time 3 hours.

  1. Answer both a and b.
    1. During the calendar year 1958 the United States “lost” over $2 billion of gold.
      1. Explain precisely what this statement means.
      2. What factors might account for the loss?
      3. What monetary or other effects does the loss have?
    2. It has been urged that to stem further losses, the U.S. should raise the price of gold from its present official level of $35 an ounce to a higher level.
      Discuss the consequences of such a move if

      1. other major countries raise the price of gold in proportion or
      2. they do not.
  2. Comment on both a and b.
    1. “Banks like to lend money. It’s their bread and butter. But sometimes loans have to be turned down. Remember, bankers are not lending their own money. Bank loans are made from money entrusted to banks by depositors.” (Business in Brief, Chase Manhattan Bank, No. 13, Oct. 1956, p. 8).
    2. “Treasury financing in 1954 was carried out with short- and intermediate-term securities, many of which were bought by commercial banks and served to increase the money supply.” Economic Report of the President, 1956.
  3. Consider a closed economy which has a fiduciary currency fixed in nominal amount. In this economy, a tax on earnings is replaced by a tax of equal yield on real property. Trace the consequences to be expected for income, interest rates, and the level of prices.
  4. Suppose all wages are escalated, in the sense of being linked continuously to a price index. It would be argued by many that government could not under such circumstances acquire real resources by issuing fiat currency. Do you agree? Justify your answer.

_______________

MONEY, BANKING AND MONETARY POLICY

Preliminary Examination for the Ph.D. and A.M. Degrees
Summer Quarter 1959
[August 4]

WRITE THE FOLLOWING INFORMATION ON YOUR EXAMINATION PAPER

Your Code Number and NOT your name
Name of Examination
Date of Examination

Results of the examination will be sent to you by letter.

Answer all questions. Time: four hours.

  1. Answer both a and b.
    1. During the calendar year 1958 the United States “lost” over $2 billion of gold.
      1. Explain precisely what this statement means.
      2. What factors might account for the loss?
      3. What monetary or other effects does the loss have?
    2. It has been urged that to stem further losses, the U.S. should raise the price of gold from its present official level of $35 an ounce to a higher level.
      Discuss the consequences of such a move if

      1. other major countries raise the price of gold in proportion or
      2. they do not.
  2. Answer either a or b.
      1. Sir John Clapham has asserted (The Bank of England, Vol. II, p. 421) that it was in the Bank of England that “the practice of central banking had originally been worked out.” To what extent do you agree?
      2. Explain and criticize what you consider the most important contribution to monetary thought before 1900.
  3. Analyze, in terms of the income-expenditure approach, the effect of a reduction in the stock of money via (a) an open market sale by the Federal Reserve, (b) a surplus in the budget used to reduce the stock of money. Indicate the empirical magnitudes that must be known to predict the quantitative effect in each case.
  4. Comment on both a and b.
    1. “Banks like to lend money. It’s their bread and butter. But sometimes loans have to be turned down. Remember, bankers are not lending their own money. Bank loans are made from money entrusted to banks by depositors.” (Business in Brief, Chase Manhattan Bank, No. 13, Oct. 1956, p. 8).
    2. “Treasury financing in 1954 was carried out with short- and intermediate-term securities, many of which were bought by commercial banks and served to increase the money supply.” Economic Report of the President, 1956.
  5. Consider a closed economy which has a fiduciary currency fixed in nominal amount. In this economy, a tax on earnings is replaced by a tax of equal yield on real property. Trace the consequences to be expected for income, interest rates, and the level of prices.
  6. Suppose all wages are escalated, in the sense of being linked continuously to a price index. It would be argued by many that government could not under such circumstances acquire real resources by issuing fiat currency. Do you agree? Justify your answer.

Source: Hoover Institution Archives. Papers of Milton Friedman, Box 77, Folder 8 “University of Chicago, Econ 331”.

Image Source: Irwin Collier taking a break from archival work at the Hoover Institution.

Categories
Chicago Economists Gender Germany Illinois Nebraska Radcliffe Wellesley Wisconsin

Michigan. Author of Progress of Labor Organization among Women, Belva Mary Herron, 1905

 

Today’s “meet an economics alumna” post features Belva Mary Herron whose only academic degree was a B.L. from the University of Michigan in 1889. Her greatest hit “Progress of Labor Organization among Women” was awarded the third Caroline Wilby Prize in 1904 “given annually to the student who has produced the best original work within any of the departments of Radcliffe College” . 

The Progress of Labor Organization Among Women, Together with Some Considerations Concerning Their Place in Industry. University of Illlinois. The University Studies Vol. I, No. 10 (May, 1905).

Herron’s only other publication I have been able to find was an article, Factory Inspection in the United States, published in the American Journal of Sociology. Vol. 12, No. 4 (January, 1907), pp. 487-99.

For the last four (or five) years of her life (she died in mid-career at age 43) she was on the faculty of Rockford College in Illinois. Between her undergraduate days and her final position at Rockford College, as best as I have been able to piece together, Belva Mary Herron wandered from the universities of Chicago, Wisconsin, Nebraska, and Illinois, then through Radcliffe and Wellesley Colleges, finding time for a year of study in Germany (1896-97). 

_____________________

Review by Edith Abbott in Journal of Political Economy (1905)

Labor Organization among Women. By BELVA MARY HERRON. (Studies of the University of Illinois.) Urbana: The University Press, 1905. 8vo, pp. 79.

A careful study of the progress of labor organization among women is a most welcome contribution to our knowledge of one of the most important phases of women’s work. Miss Herron makes no attempt in this monograph to discuss trade-unionism by and large in either its theoretical or practical aspects, but confines herself closely to a statement of the facts regarding the organizations in which women are found in the largest numbers, and a discussion of the effectiveness or lack of effectiveness of women as unionists.

After an investigation of the status of women in fourteen of the principal labor organizations affiliated with the American Federation of Labor, two questions should perhaps be raised: (i) Is there any evidence to show that women are to be considered a factor in the trade-union movement in this country today? (2) How do women differ from men as trade-unionists? A third question, as to the reasons why women should belong to unions, also suggests itself, but appears on second thought to be superfluous, for there is no special women’s problem here. There are the same advantages in organization for women as for men.

With regard to the first question, it is clear that woman’s rôle in trade-unionism is a very slight one. Though admitted into almost all the unions on the same footing as men, they have little or no influence on the organizations. Occasionally they serve as delegates to conventions, but the number of such delegates is very far from being in proportion to the number of women members. In short, it seems fair to say that women are not to be considered a factor in present-day unionism.

With regard to the differences between women and men as members of labor organizations, Miss Herron’s own statement should be quoted:

[Women] are not as well organized as men—a smaller percentage is in the union than is in the trade. Nearly all officials testify that it is harder  to organize women than men; a number say that when they once do understand union principles and become interested in the movement, they are  excellent workers; there is a unanimous opinion that there are always some capable working-women and active unionists whose good sense and enthusiasm are of great advantage to the organization. (P. 66.)

In summarizing the conditions unfavorable to women’s effectiveness in trade unions, Miss Herron regards as temporary the draw- backs which come from the “several trades ” — the low degree of  vitality and intelligence which result from miserable wages and bad sanitation; but she points out that there are other and permanent difficulties in the way — that women are the unskilled workers, and lack of vital interest in the trade; that many of them are young and do not take their industrial situation seriously; that they have more home interests; that most of them expect to marry, and regard their work as only a temporary employment, which results “in an unwillingness to sacrifice any present for a future good, as is often necessary in the union, or to give time and energy to build up an organization with which they will be identified but a few years.”

Those who have faith that there are large possibilities for women in industry, when the conventional ideas regarding women’s work shall have been readjusted, will not be inclined to regard these difficulties as “permanent” in any true sense. It may be suggested here that the largest field of usefulness for such organizations as the Women’s Trade Union League lies in attempting to remove these very difficulties. There is no ineradicable reason why women should not be given proper industrial training, and there is abundant testimony to show that they become very efficient workers with such training. Miss Herron points out that women are in industrial life to stay, and if that is true, we must help them to stay self-respectingly — as skilled laborers with a decent wage and an honest, workmanlike attitude toward their work.

On the whole, the monograph is one for which those who are interested in working-women should be grateful. It not only contains interesting and valuable information regarding women as unionists, but it also throws some much-needed light on the difference between women’s work and men’s work. In certain important industries it contains a short account of the relation of women to the earlier labor movement in the United States, a brief history of women’s trade unions in England, and sketches of organizations, like the Women’s Trade Union League, which are in sympathy with the movement for the organization of working-women.

EDITH ABBOTT.

THE UNIVERSITY OF CHICAGO.

Source: Journal of Political Economy. Vol. 13, No. 4 (September 1905), pp. 605-607.

_____________________

Personal Note (1899)

University of Nebraska.—Miss Belva Mary Herron has been appointed Instructor in Political Economy at the University of Nebraska. She was born in Pittsburg, Pa., September 23, 1866, received her early education in private schools in Mexico, Mo., and Jacksonville, Ill. And her college education in the University of Michigan, where she received the degree of Bachelor of Letters in 1889. She has subsequently pursued graduate studies at the Universities of Michigan, Chicago and Wisconsin. In 1898 Miss Herron was appointed Assistant Instructor in Political Economy.

Source: The Annals of the American Academy of Political and Social Science, Vol. 14 (November, 1899), p. 67.

_____________________

Belva Mary Herron, UM Class of ’89-’90, Lincoln Neb.
[with portrait, 1902]

Teacher in Girls’ Academy, Jacksonville, Ill., ’91. Studied in Germany ’96-’97. Fellow U. of C. ’93-’94. Instructor in Political Economy, University of Nebraska ’98-’02.

Source: The Michiganensian, 1902, p. 285.

_____________________

News from the Class of ‘89
[1910]

Belva M. Herron, ’89, who has occupied the chair of Political Economy and Political Science at Rockford College, Rockford, Ill., for the past four years, is expert agent for the United States Department of Labor. Address, Mexico, Mo.

Source: The Michigan Alumnus, Vol. XVII (November 1910). Ann Arbor, Michigan: The Alumni Association. P. 100.

_____________________

Necrology
University of Michigan
Graduates Literary Department

[Class of] 1889. Belva Mary Herron, B.L., d. at San Antonia [sic], Texas, March 4, 1911, aged 43. Buried at Mexico, Mo.

Source: The Michigan Alumnus, Vol. XVII (May 1911). Ann Arbor, Michigan: The Alumni Association. P. 496.

_____________________

University of Illinois, Alumni Record
*BELVA MARY HERRON

B.L., 1889, Univ. of Mich.; b. Sept. 23, 1866, Pittsburg, Pa.; d. John Fish (b. 1832, ibid.) & Rose (White) Herron (b. 1836, Montgomery Co., Mo.) Prepared in Jacksonville Acad., Ill. Honorary Fellowship, Univ. of Chicago, 1893-94; Fellowship, Univ. of Ill., 1904-05; Wilby prize for best work in Grad. Sch., Radcliffe Coll., 1904. Employment by Carnegie Inst. for writing history of labor laws in Ill., 1904. Teacher in Acad., Jacksonville, Ill., 1890; Asst. Instr., Adjust Prof.  in Dept. of Econ., Univ. of Nebr., 1898-1903; Asst. in Wellesley Coll., 1903-04; Fellow in Econ., Univ. of Ill., 1904-5; Instr., do., 1905-6. Author: Progress of Labor Organization among Women. *Deceased.

Source: James Herbert Kelley, ed. The Alumni Record of the University of Illinois(Urbana-Champaign: University of Illinois, 1913), p. 707.

_____________________

From Belva Mary Herron’s Last Will, May 22, 1909.

Note:  Net value of her estate ca. $18,400. Promissory notes secured by mortgages on real estate in Montgomery and Audrain counties, Missouri.

$1200 total explicitly designated for the First Christian Churches of Mexico Missouri, Lincoln Nebraska, Ann Arbor Michigan and the Christian Women’s Board of Missions of the Christian Church. $100 to the General Board of the Woman’s Christian Temperance Union.

[Following sums designated for specific individuals…] “The remainder of my estate (worth at the present time between $12000 and $13000) I will and bequeath to the Board of Home Missions of the Christian (Disciples) Church to be used preferably in building a church as settlement house some where in the middle west which might bear my mother’s name, Rose Herron Chapel.”

Source: Ancestry.com database on-line. Missouri. Probate Court (Audrain County); Probate Place: Audrain, Missouri.

Image Source: The Michiganensian, 1902, p. 285.

 

Categories
Chicago Cowles Economists

Chicago. Economics Ph.D. Alumnus, Theodore O. Yntema, 1929

 

From the records of the University of Chicago’s economics department we see that Theodore O. Yntema switched his Ph.D. thesis topic to international trade from “A Study in the Theory of Demand” after eighteen months. He was of course a very distinguished Chicago Ph.D. alumnus from the 1920s.

__________________________

Distinguished Alumni Award

THEODORE O. YNTEMA
AM ’25, PHD ’29

RETIRED CHAIRMAN, FINANCE COMMITTEE
FORD MOTOR COMPANY

Theodore O. Yntema’s ties with the University of Chicago Booth School of Business span more than five decades. After receiving an AB degree from Hope College in 1921 and an MS in chemistry from the University of Illinois in 1922, he came to the University of Chicago where he earned an AM in business in 1924 and a PhD in economics in 1929. His doctoral dissertation, a “Mathematical Reformulation of the General Theory of International Trade” published by the University of Chicago Press in 1932, was considered a classic in its field.

Yntema was a pioneer contributor not only to the development of the Booth School of Business, but also to the whole field of quantitative analysis in finance during the 1920s, 1930s, and 1940s. His career furnished a strong bond between the theoretical and analytical facets of finance and its application to modern corporate management.

He served on the faculty of Chicago Booth from 1923 until 1949, when he joined the Ford Motor Credit Company. At Ford, he was vice president of finance and subsequently became chairman of the finance committee. Yntema was a Ford director and chairman of the board for two subsidiaries, Ford Motor Credit Company and America Road Insurance Company.

He was a life trustee of the University of Chicago, a member of the Council on Chicago Booth, a professional lecturer in business policy at Chicago Booth, a visiting professor at Oakland University, a trustee of the Committee on Economic Development, and a chairman of the National Bureau of Economic Research.

The Theodore O. Yntema Professorship at Chicago Booth was established in 1973.

Source: Chicago Booth School of Business / Distinguished Alumni Awards / Honorees / Theodore O. Yntema.

__________________________

Theodore O. Yntema (1900-1985)

A.B., Hope College, 1921; A.M., 1922. and C.P.A., 1924, University of Illinois; Ph.D., University of Chicago, 1929

Theodore O. Yntema became director of research of the Cowles Commission at the time of the move to Chicago in September, 1939. [Olav Bjerkholt points out in his comment below that this is incorrect!] He joined the faculty of the University of Chicago in 1923, and was professor of statistics in the School of Business, 1930–44, and professor of business and economic policy, 1944–49. He was economic consultant in the National Recovery Administration, 1934–35; head of economics And statistics in the Division of Industrial Materials of the Defense Commission, 1940; consulting economist and statistician for the United States Steel Corporation, 1938–40; consultant in the War Shipping Administration 1942; director of research of the Committee for Economic Development, 1942–49; consulting economist for Stein Roe & Farnham, 1945–49; consulting economist, Lord, Abbett & Co., 1946–49; consulting economist, Ford Motor Company, 1947–49; and consultant for the Economic Stabilization Agency, 1951. Since 1940 Yntema has been a director of the National Bureau of Economic Research. In 1949 Yntema joined Ford Motor Company as vice president-finance and since 1950 a director of the Company. He is a Fellow of the Econometric Society and of the American Statistical Association. He is author of A Mathematical Reformulation of the Theory of International Trade, 1932, and co-author of Jobs and Markets, 1946. Yntema also directed most of the research leading to Volume I of TNEC Studies, published by the United States Steel Corporation, and from 1942–49 also planned and directed most of the research leading to the Research Reports of the Committee for Economic Development. [Abstracted from A Twenty Year Research Report 1932–1952].

Source: Cowles Foundation for Research in Economics /  From the Archives / Theodore O. Yntema (1900-1985).

__________________________

Petitions for Thesis Subject and Examination by
Theodore O. Yntema, 1926-27

March 15, 1926

Mr. T. O. Yntema
University of Chicago
Faculty Exchange

My dear Mr. Yntema:

At the last Departmental meeting it seemed to the group that the suggested topic “A Study in the Theory of Demand” is satisfactory as a thesis subject.

The fields that you suggested for the examination seemed entirely satisfactory:

  1. Theory
  2. Accounting and Statistics
  3. The Market
  4. Finance

Yours very sincerely,

LCM:MLH

*  *  *  *  *  *  *  *  *

The University of Chicago
The School of Commerce and Administration

August 20, 1927.

The Faculty of the Department of Economics:

I hereby petition for a change of my fourth field from “The Market” to “International Economic Policies”. This seems desirable in view of the change in my thesis topic from “A Study in the Theory of Demand” to “A Mathematical Reformulation of the General Theory of International Trade”. My revised list of fields would then be:

  1. Economic Theory
  2. Finance
  3. Statistics and Accounting
  4. International Economic Policies

[signed]
Theodore O. Yntema

*  *  *  *  *  *  *  *  *

[To:] Mr. T. O. Yntema

[From:] L. C. Marshall

Nov. 21, [19]27

            I am instructed to report to you that the field “International Economic Policies” meets with approval as far as the matter of general principle is concerned.

The next appropriate step is for you to prepare a detailed statement suggesting as precisely as you can what territory you intend to cover and what you contemplate preparing for the examination.

LCM: GS

Source: University of Chicago Archives. Department of Economics Records. Box 38, Folder 1.

Image Source:  Hope College. Digital Collections. History of Science at Hope College. 1921; Theodore Otte Yntema; Consulting Economist for Stein, Roe, and Farnham; Ford Motor Car Company; Lord Abbott Company.